What is Secure Multi-Party Computation?

Learn what secure multi-party computation is, how it works, and how it protects the privacy of sensitive data.

Back in the early 1980s, computer scientist and computational theorist Andrew Yao proposed a scenario few of us will ever participate in: Two millionaires go out to dinner with the agreement that the millionaire who makes the most money will be the one to foot the bill. But, while they’re dining together, they trust neither each other nor a third party with the knowledge of how much they actually make. So how do they decide who pays?

While this exact scenario is mere fantasy for most of us, its implications have real-world value – especially in a world where the privacy of sensitive personal data seems to be constantly at risk.

In this post, we’ll look at this thought experiment, as well as the history and the wider problem space of secure multi-party computation.

Yao’s Millionaire Problem

In what is truly a problem few of us will ever contend with, Yao’s Millionaire Problem nonetheless forms the foundation of the question secure multi-party computation seeks to answer:

How can multiple parties who don’t trust each other arrive at a desired output without revealing their individual inputs, even if they don’t trust a third party with calculating based on these inputs?

When it comes to data privacy, it turns out Yao’s Millionaire Problem is not so farfetched. 

As organizations collect more and more sensitive information about individuals and use that data to not only inform their metrics and strategies, but the metrics and strategies of other companies, the need for privacy-preserving sharing protocols becomes imperative. 

Two companies may not need to decide who pays for dinner, but one may want to perform computation and analysis on another company’s collected data without giving up any proprietary secrets.

To dig into this complex topic, we’ll start with a quick look at the history of secure multi-party computation.

The History of Secure Multi-Party Computation

Andrew Yao introduced his “Millionaire Problem” in Protocols for Secure Computation in 1982. More formally, the problem space is known as secure two-party computation or 2PC. 2PC was later generalized by O. Goldreich, Silvio Micali, and Avi Wigderson in their paper, How to Play ANY Mental Game, in which they expanded upon the problem posed in two-party computation and provided protocols for performing computations involving the input of multiple parties, not just two.

Since its introduction in the eighties, secure multi-party computation – also known as SMPC – has evolved into a subfield of cryptography for which a variety of protocols have been developed in order to fulfill the following two requirements in a variety of scenarios:

• Generate an output from the inputs of multiple participants
• Prevent disclosure or leakage of the inputs provided by any of the participants

Sibling Allowances: An Example of Secure Multi-Party Computation

The complexity of secure multi-party computation protocols exceeds the scope of this post, but the following is an accessible example of how secure multi-party computation works.

In this example, three siblings want to find out what the average of their weekly allowances is without revealing to each other what their individual weekly allotment is. In descending birth order, the siblings are Gabriela, Marisol, and Wanderson. Gabriela gets a weekly allowance of $15, Marisol receives $20, and Wanderson is paid $10.

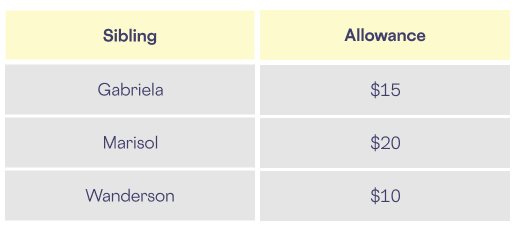
They decide to share portions of their allowance amounts among each other. Gabriela tells Marisol that she receives $10 and Wanderson that she receives $5. Marisol tells Gabriela that she receives $11 and Wanderson that she receives $1. Marisol knows the difference between those amounts and what she actually receives is $8. Wanderson tells Gabriela that he receives $5 and tells Marisol that he receives $2. Wanderson knows the difference between those amounts and what he actually receives is $3.

By adding up the individual amounts they’ve shared with each other, summing the result of that addition and then dividing by three, the siblings figure out that the average between them is $15 while remaining ignorant of the exact allowance each one receives.

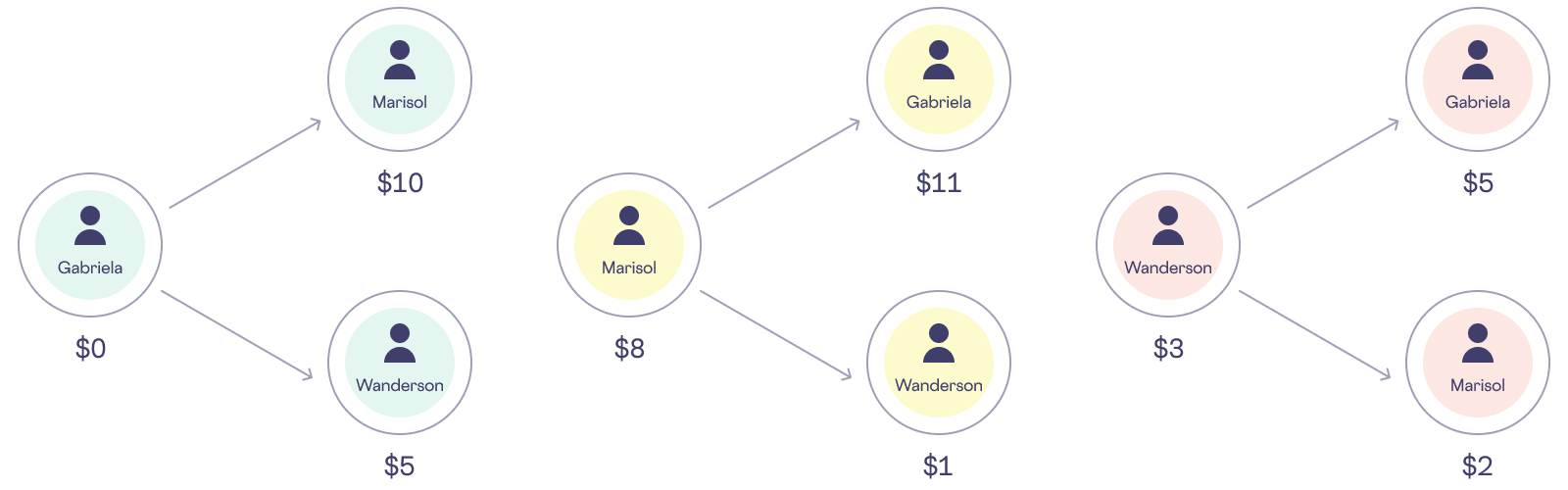
Here’s the same data shown above in tabular form, showing how the siblings could calculate their final answer while keeping their inputs confidential:

Their parents are going to have some explaining to do at the dinner table!

So Who Pays for Dinner?

In the example of the three siblings determining the average of their weekly allowances, we saw how a shared output (e.g., the average of the weekly allowances) can be determined from inputs that remain a secret (e.g., the siblings only know a portion of each other’s weekly allowance amount). However, while none of the siblings know the exact total amount of each other’s weekly allowance, they are privy to a portion of it, e.g., Wanderson knows Gabriela receives at least $5 a week.

This example also assumes that the siblings will behave honestly and will not disclose the amounts they know with each other nor try to figure out the allowance payments with the information they do have.

Meanwhile, our millionaires still have not paid for dinner and unlike the siblings, they do not trust each other or a third party. Since leaving without paying would probably get them banned from the restaurant and result in some unfavorable social media posts, how are they going to figure out who is responsible for the bill?

The following is an adaptation of a solution to the Millionaire Problem that proposes using locked suggestion boxes to figure out who makes more money without revealing either of the millionaires’ worth.

Imagine a suggestion box with a slit in the top large enough to slide a piece of paper into. Now imagine that the box can be locked with a padlock and key. Lastly, imagine that one of the millionaires – Bob – places three of these locked suggestion boxes on the dinner table. Each lock and key combination is unique, so only one key opens one lock. Each box is labeled with a dollar amount: “$1.9 million,” “$1.6 million,” and “$1.5 million.”

Unbeknownst to Alice – the other millionaire at the table – Bob is in possession of just one of the three keys. The only box Bob can unlock is the one labeled “$1.6 million” because that’s how much money he makes.

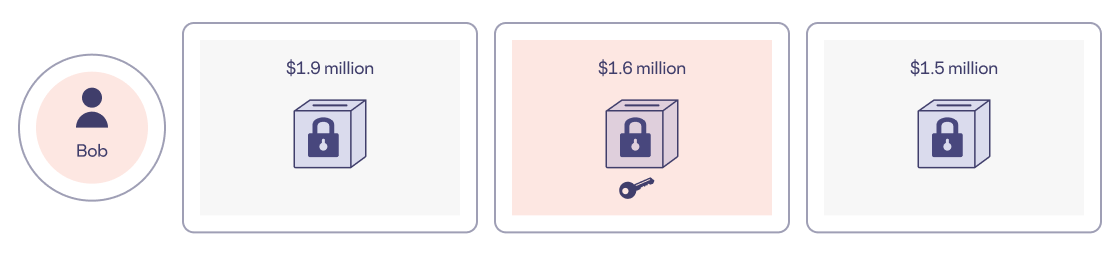
Now it is Alice’s job to insert one slip of paper into each box. On each slip of paper, she must write either “greater than” or “less than” depending on whether she makes more than or less than the amount labeled on the box. Bob excuses himself to the restroom so Alice can respond in secret. She writes, “less than” on a slip of paper and slides it into the box labeled “$1.9 million.” In the box labeled “$1.5 million,” Alice inserts a slip of paper on which she has written, “greater than.” For the box labeled “$1.6 million,” she slides in a slip of paper that reads, “greater than.”

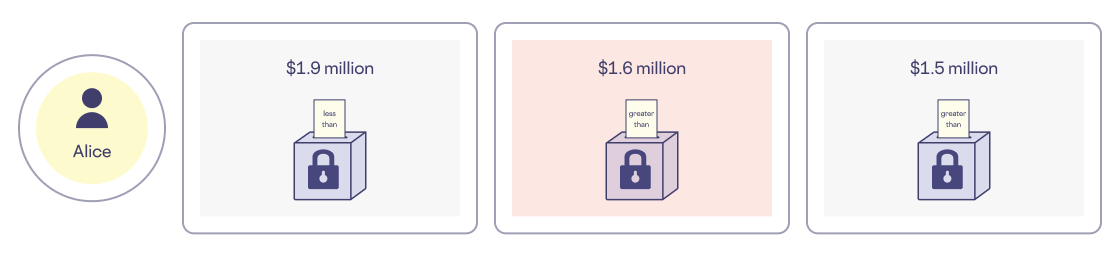
Bob returns from the restroom and now it’s Alice’s turn to leave the table. Bob uses his key to unlock the box labeled “$1.6 million” and sees that Alice’s response is “greater than.” Now Bob knows that since Alice makes more money than he does, she’s the one who is going to be paying for dinner. However, while Bob knows that Alice is the richer one between the two of them, he does not know how much she makes, and nor does Alice know Bob’s worth.

When Alice returns to the table, Bob informs her that she will be paying the bill. They have a lovely dinner and Alice leaves a generous tip for the waiter.

The Role of SMPC in Data Privacy

As you’re no doubt well aware, our personal information has become one of the hottest commodities in the digital age. The advent of cloud computing means that companies can easily store and access ever increasing amounts of  data. However, with the rise of privacy regulations like the EU’s GDPR, the frequency of data breaches and the upcoming deprecation of third-party cookies, companies need new solutions to enable the use of sensitive data while still protecting it.

That’s where secure multi-party computation comes in.

The above two examples show us how secure multi-party computation can work, but neither of these examples is likely to occur in the real world.

A more realistic scenario for SMPC is advertising. Data clean rooms are a response to the demise of third party tracking cookies. A data clean room enables brands and advertisers to perform operations on user data that has been sanitized (or de-identified), removing any sensitive, personally identifiable information. In such an environment, the first-party data of multiple parties is collected, aggregated, and anonymized so other parties can generate outputs based on this data while remaining compliant with privacy laws.

For instance, a hardware company that produces padlocks and keys for suggestion boxes is considering a new advertising campaign to air during podcasts. In particular, they want to target millionaire podcast audiences. The hardware company can implement a data clean room compiled of user information from various podcast streaming services. 

With this aggregate of data, the hardware company learns that subscribers whose information overlaps with demographics common among millionaires also overlaps with certain podcasts. The hardware company decides to partner with those particular podcasts to advertise their suggestion box padlocks and keys. This use case is similar to the previous example involving sibling allowances.

More complex use cases for secure multi-party computation occur in research and encryption key management. SMPC can be especially useful for machine learning. In this case, SPMC enables AI models to train on data without revealing proprietary intellectual property such as the algorithms the model is composed of or compromising the privacy of the individuals the data was collected from – data which could potentially identify them.   

Similarly, secure multi-party computation can allow for better protection of encrypted data with key management. In this particular scenario, a company might use SMPC as part of their privacy strategy to generate keys and encrypt and decrypt data. The end result is a set of encryption keys that each decrypt only a portion of data, creating a challenge for attackers by limiting what they can actually steal.

Secure Multi-Party Computation Is Still in Its Infancy, but Privacy Concerns Are Pressing 

Even though the concept was introduced in the 1980s, it wasn’t until the early 2000s that SMPC developed from theory to practice. The first large-scale and practical application of multi-party computation was the execution of an electronic double auction in the Danish Sugar Beet Auction, which took place in January 2008. 

You can see how the solution to the Millionaire’s Problem becomes exponentially more complex as more parties and data become involved. In other words, if a group of millionaires decide to go out to dinner and agree to pay for it under the same constraints as those applied to Bob and Alice, it quickly becomes impractical to bring a set of suggestion boxes, padlocks, keys, and slips of paper to the table – moreover, it’s quite the faux pas. For now, the millionaires will have to trust a third party to ensure their privacy.

Fortunately, Skyflow has solutions for even the most complex data privacy challenges.

Skyflow Lets You Achieve Privacy by Design

Skyflow Data Privacy Vault is a comprehensive solution to protecting the privacy and security of sensitive data through techniques like encryption, tokenization, masking, and fine-grained data governance. Available via an API, Skyflow helps to ensure the privacy of sensitive information and eases compliance without sacrificing data utility. Skyflow provides a way to implement privacy by design principles to companies looking to improve their privacy posture or build for data privacy from day one.

To learn about data privacy vaults and how they can fit into your tech stack, read more from Skyflow’s Field CTO, Manish Ahluwalia. 

To find out what makes a data privacy vault, check out “Five Essential Ingredients of a Data Privacy Vault.” 

You can check out Skyflow’s tokenization, encryption, and other features when you sign up to try Skyflow.

‍